贝塞尔曲线
De Casteljau算法
由(n+1)个控制点定义的n次贝塞尔曲线可被定义为由前n个、后n个控制点定义的两条(n-1)次贝塞尔曲线的线性组合。
$P_0^n = (1-t)P_0^{n - 1} + t P_1^{n-1}$
得到递推公式:
$P_i^k = (1-t)P_i^{k-1} + tP_{i+1}^{k-1} (k=1,2,3,..n)(n=0,1,2…n-k)$
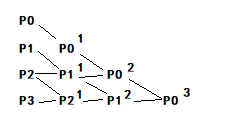
曲线方程
二阶贝塞尔曲线:
$P_0^2(t) = (1-t)^2P_0 + 2t(1-t)P_1 + t^2P_2$
N阶贝塞尔曲线:
$P_0^n(t) = Σ_{j=0}^n P_jB_j^n(t)$
贝塞尔曲线的性质
- 曲线起点终点与控制点重合,与起始、终止线段相切。
- 对贝塞尔曲线做仿射变换等同于对控制点做仿射变换。
- 凸包性质:贝塞尔曲线一定在控制点的凸包内部。
逐段贝塞尔曲线
一般用三阶贝塞尔曲线(即4控制点)为一段拼接起来。
B样条和NURBS
B样条是贝塞尔曲线的一般化。
B样条有局部性、几何不变性、凸包性、保凸性。
(待补充)
贝塞尔曲面
(待补充)
(END)